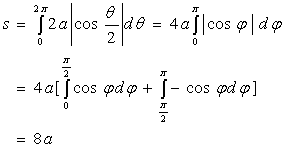§6.4 平面曲线的弧长

一、直角坐标情形

设函数在区间上具有一阶连续的导数，计算曲线的长度。

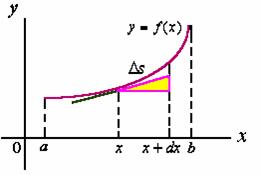
取为积分变量，则,在上任取一小区间，那么这一小区间所对应的曲线弧段的长度可以用它的弧微分来近似。

于是，弧长元素为

弧长为

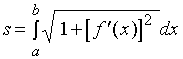
【例1】计算曲线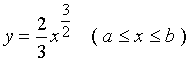的弧长。

解：

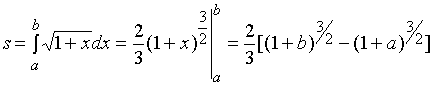
二、参数方程的情形

若曲线由参数方程

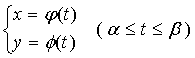
给出，计算它的弧长时，只需要将弧微分写成

的形式，从而有

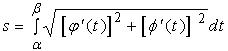
【例2】计算半径为的圆周长度。

解： 圆的参数方程为

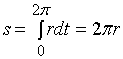
三、极坐标情形

若曲线由极坐标方程

给出，要导出它的弧长计算公式，只需要将极坐标方程化成参数方程，再利用参数方程下的弧长计算公式即可。

曲线的参数方程为

此时变成了参数，且弧长元素为

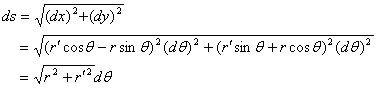
从而有

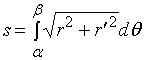
【例3】计算心脏线的弧长。

解：